Die Naturwissenschaften haben sich in den letzten zwei Jahrhunderten zu ungeahnten Höhen aufgeschwungen. Der analysierende Verstand des Menschen dringt dabei immer tiefer in das Reich der Natur ein, vom Mikro- bis zum Makrokosmos. Das von den Naturwissenschaften generierte Wissen dient nicht nur zur Befriedigung unserer Neugierde über die Welt, sondern ist zudem Grundlage für neue Technologien und somit Motor der Wirtschaft.
Auch die Philosophie hatte einst den Anspruch geltend gemacht, Wahres, Allgemeingültiges über die Natur auszusagen. Nur ist ihre Erfolgsgeschichte weniger geradlinig und glänzend verlaufen als die der Naturwissenschaften. Die Naturphilosophie, deren europäische Wurzeln im antiken Griechenland liegen und die als Hebamme der Naturwissenschaften gilt, hat ihren neuzeitlichen Höhepunkt in Schelling und Hegel gefunden, der aber zugleich den Beginn ihres Abstieges wenn nicht gar Untergangs markiert.

Die Naturphilosophie wird und wurde von der Naturwissenschaft selten ernst genommen, meistens mit Spott bedacht. „Zu spekulativ, viele sogenannte Beweise für die Existenz Gottes oder einer Seele seien erschlichen, Taschenspielertricks, …“ lauten oft (nicht immer ganz zu Unrecht) die Vorwürfe. Auch Kant, aus den eigenen Reihen der Philosophen, hat sich dahingehend geäußert.
Der große Erfolg der Naturwissenschaften ist vor allem darauf zurückzuführen, dass es gelungen ist, bestimmte Bereiche des Naturgeschehens mithilfe der Mathematik zu modellieren (abzubilden) und daraus resultierende Behauptungen im Experiment zu verifizieren.
Immer wieder hat es Versuche gegeben, die Mathematik auch für die Philosophie dienstbar zu machen. Schon Platon hat auf die große Bedeutung der Mathematik für das philosophische Denken hingewiesen. Aber alle bisherigen Versuche, eine „more geometrico“ (lat. nach Art der Geometrie) in der Philosophie zu etablieren, müssen als wenig erfolgreich bezeichnet werden. Dieses manchmal fast gewaltsame hineinzwängen mathematischer Systeme in die Philosophie nimmt dabei schnell den Charakter okkulter Zahlenmystik an.
Während die Naturwissenschaft auf das strenge aber enge Korsett mathematischer Logik zurückgreifen kann, ist die Philosophie in ihrem „Alltagsgeschäft“ auf die weniger präzise aber dafür sehr umfassende „Gebrauchssprache“ (angereichert um philosophische Begriffe und somit auch Fachsprache) und ihre immanente Logik angewiesen.
Wenn nun das in zweieinhalb Jahrtausenden Naturphilosophie, von Thales bis Hegel, Gesagte und Geschriebene nicht alles Unsinn sein soll, und sich hinter ihrer oft schillernden Sprache ein wahrer Kern verbirgt, dann muss (unserer Überzeugung nach) auch eine gemeinsame (mathematische) Sprache existieren, in der sich Naturwissenschaften und Naturphilosophie begegnen. Es gibt nur eine Natur, der Kosmos in dem wir alle leben, aber es existieren viele verschiedene Möglichkeiten, darüber zu sprechen: in Form mathematischer Logik, in der Gestalt künstlerischer oder philosophischer Betrachtungen …

Warum sich dabei gegenseitig bekämpfen? Keine dieser Perspektiven kann den Anspruch auf alleinige Vollständigkeit erheben. Warum nicht im Sinne von These und Antithese nach einer Synthese suchen? Warum nicht die naturwissenschaftliche mit der philosophischen zu einer umfassenderen Perspektive vereinen? Solch eine „Tieferlegung der Fundamente“ wurde bereits in den letzten Lexikonpunkten begonnen und soll jetzt fortgeführt werden.
Ein guter Ansatzpunkt dafür findet sich in den Begriffen Raum, Zeit und Materie. Dass diese Dreiheit in der Physik (die wohl erfolgreichste Naturwissenschaft) eine zentrale Rolle spielt, muss wohl kaum betont werden. Um zu zeigen, wie weit die naturwissenschaftliche und philosophische Betrachtung der Begriffe Raum, Zeit und Materie zunächst auseinander liegen, ist kein Philosoph besser geeignet als Immanuel Kant. Kant definiert in der „Kritik der reinen Vernunft“:
– „Der Raum ist nichts anderes, als nur die Form aller Erscheinungen äußerer Sinne, d.i. die subjektive Bedingung der Sinnlichkeit, unter der allein uns äußere Anschauung möglich ist.“
– „Die Zeit ist nichts anderes, als die Form des inneren Sinnes, d.i. des Anschauens unserer selbst und unseres inneren Zustandes.“
– „ … die Materie (das Physische), oder der Gehalt, welcher ein Etwas bedeutet, das im Raume und der Zeit angetroffen wird, mithin ein Dasein enthält und der Empfindung korrespondiert.“
Raum und Zeit sind bei Kant universelle Formen (Strukturen) des Bewusstseins, die durch das einheitsstiftende „Ich bin“ der transzendentalen Apperzeption verbunden sind.
Materie, als ein empirisches Phänomen des wahrnehmenden Bewusstseins, ist eine in der Erscheinung gegebene, zunächst unbestimmte Mannigfaltigkeit, die durch solch subjektive (aber universelle!) Formen (wie Raum und Zeit) erst bestimmt werden muss.
In den Formulierungen der Physik wird hingegen versucht, alles Subjektive zu vermeiden, und objektive, d.h. allgemeine, beobachterunabhängige Gesetzmäßigkeiten zu formulieren. In den Naturwissenschaften steht subjektiv für: nicht objektiv, persönlich, einseitig, nicht neutral, unsachlich, verzerrt, voreingenommen, tendenziös …
In der Philosophie bedeutet der Begriff Subjekt jedoch „das Zugrundeliegende“ (die Unterlage, der Träger, griech. hypokéimenon). Die Einheit der transzendentalen Apperzeption, das transzendentale Ich, ist für Kant der wahre Grund für die Möglichkeit objektiver Wissenschaften und warum diese sich mithilfe der Mathematik überhaupt formulieren lassen (Kopernikanische Wende in der Philosophie, Revolution der Denkart).
Raum, Zeit und Materie in der Physik
Der Raum war bis zu Einsteins Allgemeiner Relativitätstheorie der starre, unveränderliche Hintergrund, die unendlich große Bühne, auf der die Akteure, die Materie, durch Kräfte bewegt, ihr kosmisches Drama aufführen. Um dieses Geschehen mithilfe der Mathematik beschreiben zu können, muss zunächst im Raum ein Koordinatensystem errichtet werden: 3 zueinander senkrechte Geraden (Achsen), die sich in einem Punkt schneiden. Dieser Schnittpunkt (Koordinatenursprung, Nullpunkt) symbolisiert den Ort eines Beobachters (Zuschauers) des physikalischen Geschehens. Mithilfe eines solchen Koordinatensystems kann jeder Punkt des Raumes durch ein Zahlentripel (x, y, z) identifiziert werden. Die Zeit selbst wird als eine externe, von allem Geschehen unabhängige Gerade dargestellt.
Isaac Newton hat über den Raum und die Zeit gesagt:
„Der absolute Raum bleibt vermöge seiner Natur und ohne Beziehung auf einen äußeren Gegenstand stets gleich und unbeweglich.“
„Die absolute, wahre und mathematische Zeit verfließt an sich und vermöge ihrer Natur gleichförmig und ohne Beziehung auf irgendeinen äußeren Gegenstand.“
Newton hat Raum und Zeit aber auch als ein Sensorium (lat. Gesamtheit aller Sinne) Gottes bezeichnet.
Wie sieht es nun mit der Objektivität des physikalischen Geschehens aus? Zunächst ist zu sagen, dass jeder Beobachter sich an einem anderen Ort befindet, in eine andere Richtung schaut, der eine steht, der andere geht … Darum wird jeder dieser Beobachter dasselbe Geschehen ein wenig anders wahrnehmen.
Also sind die physikalischen Theorien, wie hier die Klassische Mechanik, doch nicht so objektiv, sondern eher subjektiv, beobachterabhängig? Ja und Nein.
Zunächst sind die Messdaten beobachterabhängig. Ein Astronom auf der Erde wird andere Bahnkurven der Planeten messen als ein Astronom nahe der Sonne. Nun gibt es in der Klassischen Mechanik die sogenannten Galilei-Transformationen. Diese haben eine gewisse Dolmetscherfunktion zwischen verschiedenen Beobachterperspektiven. Habe ich als ein Beobachter A eine Messreihe durchgeführt und möchte nun wissen, was ein Beobachter B misst (der sich an einem anderen Orte befindet, in eine andere Richtung schaut und sich mit konstanter Geschwindigkeit bewegt), dann kann ich mittels der Galilei-Transformationen meine Messdaten umrechnen und weiß so, was Beobachter B messen wird. Oder es kann von vorneherein mithilfe der Galilei-Transformationen (die den Umfang möglicher Beobachter-Perspektiven innerhalb der Newtonschen Mechanik repräsentieren) gefragt werden: Welche physikalischen Größen sind beobachterunabhängig, sind invariant gegenüber einem Beobachter-, einem Perspektivenwechsel? (invariant: bei veränderten Bedingungen unverändert bleibend)
Oder mit den Worten Felix Kleins und seinem Erlanger Programm:
„Es ist eine Mannigfaltigkeit und in derselben eine Transformationsgruppe gegeben; man soll die der Mannigfaltigkeit angehörigen Gebilde hinsichtlich solcher Eigenschaften untersuchen, die durch die Transformationen der Gruppe nicht geändert werden.“
Oder kürzer:
„Es ist eine Mannigfaltigkeit und in derselben eine Transformationsgruppe gegeben. Man entwickele die auf die Gruppe bezügliche Invariantentheorie.“
Das heißt aber auch, dass im Wesentlichen die jeweilige Transformationsgruppe einer Geometrie (wie z.B. die Galilei-Transformationen der Newtonschen Raum-Zeit) dafür bestimmend ist (philosophisch gesprochen: die Form dafür ist), was innerhalb einer Theorie als eine sinnvolle geometrische bzw. physikalische Eigenschaft (Größe) zu gelten hat. An dieser Stelle lässt sich vielleicht schon erahnen, dass die Kantschen apriorischen Formen des Bewusstseins Raum und Zeit (welche die Mannigfaltig der Materie ordnen) und die Kleinschen Transformationsgruppen (mit ihren Invarianten einer Mannigfaltigkeit), welche die Beobachterperspektiven repräsentieren, nicht soweit auseinander liegen, wie es zunächst erscheinen mag.
Nun hat sich gezeigt, dass die Newtonsche Mechanik mit ihrer Raum-Zeit nur eine gute Näherung für Geschwindigkeiten ist, die um vieles kleiner sind als die Lichtgeschwindigkeit c. Durch die Spezielle Relativitätstheorie wurde ein Bühnenumbau notwendig. An die Stelle des 3-dimensionalen (Abk. –dim) Euklidischen Raumes und der 1-dim Zeit trat die 4-dim Raumzeit des Minkowski Raumes mit pseudo-Euklidischer Metrik. Zusätzlich mussten die Galilei-Transformationen durch die Poincaré-Transformationen ersetzt werden.
Die Gravitationsgleichungen der Allgemeinen Relativitätstheorie und die Entdeckung, dass das Universum expandiert, machten jedoch schon bald einen neuerlichen Umbau notwendig: Das sich ausdehnende Universum wird besser durch einen deSitter Raum (auch deSitter Raumzeit genannt) beschrieben.

Der deSitter Raum
Spätestens seit Einsteins Allgemeiner Relativitätstheorie ist deutlich geworden, dass das bisherige Vorgehen physikalischer Theoriebildung problematisch ist: d.h. zuerst eine feste Raum-Zeit-Struktur als Bühne festzulegen und diese dann nachträglich mit Materie und Kräften „aufzufüllen“. Denn wie die Einsteinschen Gleichungen zeigen, sind Raum, Zeit und Materie wechselseitig bedingt. Hermann Minkowski, ein Lehrer Einsteins, sagte über die nach ihm benannte 4-dim Raumzeit in seinem Vortrag „Raum und Zeit“ (gehalten auf der 80. Naturforscherversammlung zu Köln, 1908): „Von Stund′ an sollen Raum für sich und Zeit für sich völlig zu Schatten herabsinken und nur noch eine Art Union der beiden soll Selbständigkeit bewahren.“
Aber erst eine physikalische Theorie, in der die Materie mittels der Koordinate einer 5. Dimension innerhalb eines 5-dim Raum-Zeit-Materie Kontinuums beschrieben werden kann, ist eine wahre Union. START (Space-Time-Action Relativity Theory von Jaime Keller) erlaubt eine solche wirklich einheitliche Konstruktion in der Physik, aber dazu später mehr.
Der deSitter Raum soll zuerst kurz aus der Sicht Albert Einsteins betrachtet werden und dann aus der Felix Kleins. Albert Einstein zeigt uns die helle, bunte und detailreiche Oberfläche des „globus intellectualis“ (eine von Francis Bacon – engl. Philosoph, 1561-1626 – eingeführte Metapher), während wir mit Felix Klein in das geheimnisvolle Halbdunkel seines Inneren vordringen werden.
I. Albert Einstein:
Die Gravitationsgleichungen der Allgemeinen Relativitätstheorie haben folgende Gestalt:
oder kürzer
Dabei ist der Ricci-Tensor,
der metrische Tensor,
der Energie-Impuls-Tensor und
der geometrische Tensor oder Einsteintensor.
Das ist ein System nichtlinearer partieller Differentialgleichungen für die Koeffizienten der Metrik und ihre ersten beiden Ableitungen. Die Gleichungen zeigen den engen Zusammenhang zwischen der Verteilung der Materie im Raum (dargestellt durch den Energie-Impuls-Tensor
) und der metrischen Struktur
der Raumzeit.
Einstein war zunächst der Meinung, dass aufgrund der Kompliziertheit der Gleichungen keine exakte Lösung zu finden sei. Aber bereits ein Jahr später gelang Schwarzschild, mithilfe die Gleichungen stark vereinfachenden Annahmen, eine erste Lösung. Als Einstein erkannte, dass seine Gleichungen kein statisches Universum zulassen würden, fügte er den Gravitationsgleichungen eine sogenannte Kosmologische Konstante hinzu.
Damals stand das Universum noch als ein Sinnbild für das Ewige, Unvergängliche und somit Statische (eine Nachwirkung der Antike und des Mittelalters).
Aber auch mit einer genau eingestellten Kosmologischen Konstante lässt sich höchstens ein instabiles statisches Universum erreichen. Diese Tatsache zusammen mit der kurz darauf erfolgten Beobachtung, dass das Universum tatsächlich expandiert, veranlasste Einstein, die Kosmologische Konstante wieder zu verwerfen.
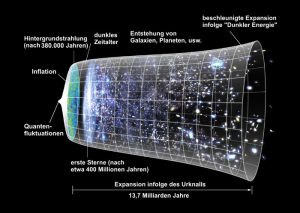
Heute spricht vieles für die Existenz einer solchen Kosmologischen Konstante. Mit ihr lässt sich schlüssig die inflationäre Phase kurz nach dem Urknall (eine Phase extrem schneller Ausdehnung) und – die kürzlich mithilfe eines bestimmten Typus von Supernova gemessene – aktuelle beschleunigte Expansion des Universums erklären. Zudem ist die rätselhafte Dunkle Energie ein sehr wahrscheinlicher Kandidat für die Kosmologische Konstante.
Die deSitter Raumzeit ist nun die maximal symmetrische Vakuumslösung () der Einsteinschen Gravitationsgleichungen mit positiver (repulsiver) Kosmologischer Konstante
. Die deSitter Raumzeit wurde 1917 von Willem de Sitter (niederl. Astronom, 1872-1934) und unabhängig davon durch Tullio Levi-Civita (ital. Mathematiker, 1873-1941) entdeckt.
Zur Fortsetzung: Horizonte 9 – Teil B 〉〉〉