Horizonte 9 – Teil C (Takimo 32)

Die Gravitationsgleichungen der Allgemeinen Relativitätstheorie haben 3 Raumkoordinaten (x, y, z) und 1 Zeitkoordinate t. Bei gegebener Materieverteilung wird zunächst der Energie-Impuls-Tensor T_{ \mu \nu} konstruiert. Eingesetzt in G_{ \mu \nu} = \kappa T_{ \mu \nu} ergeben sich Differenzialgleichungen für die metrischen Koeffizienten g_{ \mu \nu}. Gelingt es, diese zu lösen, ist damit auch die Metrik der Raumzeit bestimmt, d.h. es ist eine Vorschrift gegeben, wie Raum- und Zeitabstände zu messen sind. Mit der Metrik der Raumzeit ist aber im wesentlichen auch die Dynamik bzw. Physik bestimmt. Denn bei gegebenen metrischen Koeffizienten g_{\mu\nu}, und damit auch dem Linienelement \mathrm{d}s (infinitesimales Wegelement) und den Christoffelsymbolen \Gamma_{\mu\nu}^\sigma, lassen sich mithilfe der Geodätengleichung

\frac {\mathrm{d}^2 x^\sigma}{\mathrm{d}s^2} -\Gamma_{ \mu \nu}^\sigma \frac {\mathrm{d} x^\mu}{\mathrm{d}s}\frac {\mathrm{d} x^\nu}{\mathrm{d}s} = 0

die entsprechenden Bahnkurven x(s) berechnen. Das sind die (lokal) kürzesten Verbindungskurven zwischen Punktpaaren und sie entsprechen im Euklidischen Raum den Geraden.

Es ist aber auch möglich, wie im Falle des deSitter Universums, Lösungen der Gravitationsgleichungen in einem 6-dim Projektiven Raum zu entwerfen. Wie im vorangegangenen Lexikonpunkt geschehen, wird darin zunächst eine 5-dim Minkowski Raumzeit konstruiert. Diese enthält ein 5-dim Hyperboloid, auf dessen 4-dim Oberfläche mittels geeigneter Koordinatenwahl die Metrik des deSitter Universums festgelegt wird. Nach heutigem Erkenntnisstand leben wir in einem solchen Universum mit annähernd flacher Metrik und exponentieller Expansion.

Die Erde ist ein gutes niederdimensionales Anschauungsmodell für ein deSitter Universum. Denn wie die Erdoberfläche durch einen (annähernd) festen Radius (X_1^2 + X_2^2 + X_3^2 = R^2, mit R als Erdradius) definiert ist, so ist auch das deSitter Universum als eine 4-dim Oberfläche, durch einen konstanten Abstand X_1^2 + X_2^2 + X_3^2 - X_4^2 + X_5^2 = \frac{3}{\Lambda} =: R^2 (Kosmologische Konstante \Lambda) zu einem Mittelpunkt bestimmt.
Um bei dem Beispiel der Erde zu bleiben, treiben wir auf einem Ozean Dunkler Energie. Die Planeten und Galaxien sind darauf nur Schaumkronen bzw. kleine Inseln aus „normaler“ Materie.

Ozean_aus_dunkler_Energie
Die Dunkle Energie des Universums ist gleich dem Wasser eines Ozeans. Die uns sichtbare „normale Materie“ entspricht in diesem bildhaften Vergleich den winzigen Schaumkronen und die Galaxien kleinen Inseln. Die Dunkle Materie ist mit Landmassen vergleichbar, die verborgen unter der Wasseroberfläche liegen.

Die 5. und 6. Dimension eines 6-dim Projektiven Raumes, die in den Gleichungen der Allgemeinen Relativitätstheorie gar nicht vorkommen, erlauben es, die „Oberfläche“ zu verlassen und auf eine mathematisch fundierte Weise in das Innere des Globus, des „globus intellectualis“ zu gelangen, dorthin, wo die Philosophie zu Hause ist.

 

Raum-Zeit-Materie-Evolution

(lat. evolvere: auswickeln, entwickeln)

Was aber ist die 5. und 6. Dimension? Wie hat man sich diese vorzustellen? Etwas vorgreifend soll so viel gesagt sein:

Neben den 3 Raumdimensionen (1. bis 3. Dimension) und 1 Zeitdimension (4. Dimension) ist die 5. Dimension eine eigenständige Dimension der Materie und Energie (genauer: eine Dimension der Wirkungsdichte).

Und die 6. Dimension ist im Gegensatz zur reversiblen, physikalischen Zeit (4. Dimension) eine irreversible Zeit. Diese 6. Dimension ist eine Zeit, die Geschichte und Evolution in das Universum bringt.

Diese zwei unterschiedlichen Zeitdimensionen haben ihre Entsprechungen in der Zeittheorie des englischen Philosophen McTaggart (1866-1925). Sein Beweis, dass die Zeit eine Illusion sei, gilt zwar als gescheitert, aber die auf ihn zurückgehende Klassifizierung der Zeit in drei Zeitreihen A, B und C ist heute Standardterminologie.

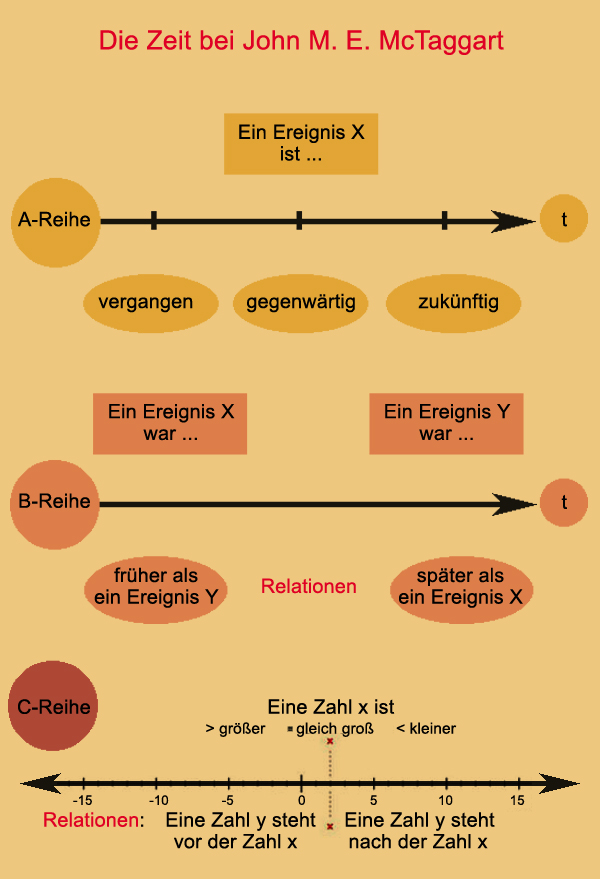
McTaggart_Zeitreihe

1908 veröffentlichte John M. E. McTaggart den Aufsatz „The unreality of Time“. Es ist einer der einflussreichsten Texte der neueren Zeitphilosophie. Darin unterscheidet McTaggart zwischen verschiedenen Betrachtungsweisen der Zeit, der A-, B- und C-Reihe. (Bild: Polaris Hörspiele)

Die 6. Dimension (in ihrem projektiven Aspekt) würde nach dieser Einteilung der A-Reihe entsprechen. Die A-Reihe operiert mit den Begriffen „vergangen“, „gegenwärtig“ und „zukünftig“ und ist auf die subjektive Perspektive der ersten Person eines Sprechers bezogen. In Kants Transzendental-Philosophie wären das die Zeitmodi auf der Ebene der Anschauungsformen.
Die B-Reihe beinhaltet hingegen Begriffe wie „früher als“, „gleichzeitig“ und „später als“ und korrespondiert mit Kants Zeitbestimmung der transzendentalen Schemata. Zusammen mit der C-Reihe (diese hat eine Ordnungsstruktur „größer“ und „kleiner“ wie die Natürlichen Zahlen) bildet sie die objektive, physikalische Zeit.

Aber auch Henri-Louis Bergson (frz. Philosoph, 1859-1941) unterschied zwei verschiedene Zeittypen: la durée und le temps.
La durée, die Dauer, bezeichnet die subjektive, erlebte Gegenwart. Diese erlebte Gegenwart, die für sich nur ein ausdehnungsloser Punkt wäre, ist mit vergangenen, gegenwärtigen und zukünftigen Vorstellungen verflochten und erhält durch das begleitende „Ich lebe“, das „Ich bin“ der transzendentalen Apperzeption, Einheit und Dauer.
Le temps hingegen ist die objektive, physikalische Zeit. In kosmologischen und atomaren Modellen der Naturwissenschaften tritt sie als 4. Dimension der Minkowski Raumzeit in Erscheinung.

Der Philosoph Martin Heidegger (1889-1976) unterschied ebenfalls eine ursprüngliche Zeit bzw. Weltzeit (Innerzeitigkeit) und eine vulgäre Zeit (die gemessene Uhr-Zeit).

Die 5. und 6. Dimension eines 6-dim Projektiven Raumes öffnen das Tor zum Verständnis, wie subjektive, apriorische Anschauungs- und Denkformen eines transzendentalen Ichs das eigentliche Fundament objektiver Naturwissenschaften sein können.

Über diese 6. Dimension wird noch genauer gesprochen, nachdem die Raumzeit durch Hinzunahme von Spiegelungen (Inversionen als Transformationen) zu einer konformen Raumzeit erweitert wurde.

 

START

Zunächst aber noch etwas über die 5. Dimension in physikalischer Hinsicht, d.h. als eine metrische Größe. Jaime Keller (mexik. Physiker, 1936–2011) hat in seiner START Konzeption die Wirkungsdichte als Koordinate einer 5. Dimension eingeführt. Dabei greift er auf Arbeiten von Yuri Borisovich Rumer (sowj. Physiker, 1901-1985) aus den Jahren 1920 bis 1940 zurück. In START (Space-Time-Action Relativity Theory) wird die Physik nach einem sehr einheitlichen Prinzip aufgebaut. Dies geschieht in einem ebenfalls 5-dim Minkowski Raum, wie bei der Konstruktion des deSitter Universums im vorangegangenen Lexikonpunkt, nur wird dabei nicht auf den projektiven Hintergrund Bezug genommen. Der projektive Hintergrund ist aber für den Erfolg, in das Innere des „globus intellectualis“ vorzudringen und auf diesem Wege Kants Transzendental-Philosophie zu finden, von entscheidender Bedeutung. Trotz dieser Einschränkung hilft uns START zu verstehen, was die 5. Dimension ist.

Anschaulich geht die START Konstruktion wie folgt vor sich. Ausgangspunkt ist wie bereits erwähnt eine 5-dim Minkowski Raumzeit. Als erster und wichtigster Punkt gilt es, die, je nach vorgegebener physikalischer Gegebenheit, entsprechende Wirkungsdichte a(x,y,z,t) (engl. action density) zu konstruieren. Die Wirkungsdichte ist die Wirkung A dividiert durch das 4-dim Volumenelement: a = \frac{A}{\Delta x \Delta y \Delta z \Delta t}. Da die Wirkung so etwas wie Energie mal Zeit ist und eingesetzt sich die Zeit rauskürzt, kann die Koordinate in Richtung der 5. Dimension auch als eine räumliche Energie- bzw. Materiedichte angesehen werden. Exakt betrachtet ist die Wirkungsdichte a(x, y, z, t) das Pseudoskalar einer Clifford-Algebra.

Eine Zwischenbemerkung:
Das bekannte Zitat von Hermann Minkowski „Von Stund′ an sollen Raum für sich und Zeit für sich völlig zu Schatten herabsinken und nur noch eine Art Union der beiden soll Selbständigkeit bewahren.“ wurde bereits im vorletzten Lexikonpunkt erwähnt. Weniger bekannt ist das Zitat aus dem gleichen Vortrag: „Um nirgends eine gähnende Leere zu lassen, wollen wir uns vorstellen, daß aller Orten und zu jeder Zeit etwas Wahrnehmbares vorhanden ist. Um nicht Materie oder Elektrizität zu sagen, will ich für dieses Etwas das Wort Substanz brauchen.“
Diese Substanz entspricht ziemlich genau der Wirkungsdichte a(x, y, z, t) aus START, nur dass Minkowski seine Substanz nicht in den Status einer Extradimension erhoben hat. Übrigens ist H. Minkowski der Erfinder der 4-dim Raumzeit und nicht wie öfters urtümlich angenommen A. Einstein.
Ende der Zwischenbemerkung

Wichtig ist, dass die Wirkungsdichte a(x, y, z, t) in der 5-dim flachen Raumzeit eine 4-dim Mannigfaltigkeit bildet (wie das Hyperboloid des deSitter Universums), auf der die gesamte Dynamik stattfindet. Als Nächstes gilt es, das Linienelement ds und damit die Metrik auf der durch a festgelegten Mannigfaltigkeit zu bestimmen.

-\,\mathrm{d}s^2 = \mathrm{d}x^2 + \mathrm{d}y^2 + \mathrm{d}z^2 - \mathrm{d}t^2 + \mathrm{d}a^2   (Bemerkung siehe Fußnote *)

Nun ist ein anderes wesentliches Postulat von START, dass die Längen der Bahnkurven minimal (d.h. Geodäten) sind. Ist die Metrik mittels der Wirkungsdichte a(x, y, z, t) und der Formel g_{ \mu \nu} = \frac{\partial X^i }{\partial x^\mu} \frac{\partial X^j }{\partial x^\nu}G_{ij} erst einmal bestimmt, können (wie in der Allgemeinen Relativitätstheorie) mithilfe der Geodätengleichung solche Bahnkurven berechnet werden.

In der üblichen 4-dim Minkowski Raumzeit (Speziellen Relativitätstheorie) gilt Folgendes: Das Licht bewegt sich mit Lichtgeschwindigkeit c im 3-dim Raum. Gegenstände mit einer von Null verschiedenen Masse bewegen sich immer mit einer Geschwindigkeit kleiner als c, da sonst die Energie unendlich groß wäre.

Wie sieht diese Situation in der 5-dim Minkowski Raumzeit aus? Objekte bewegen sich nach START immer mit Lichtgeschwindigkeit c auf der durch a(x, y, z, t) festgelegten Mannigfaltigkeit. Geodäten von Licht haben die kürzestmögliche Länge, nämlich 0. Das bedeutet \mathrm{d}s = 0 und aus der obigen Gleichung für das Linienelement folgt  c^2 = v_{x}^2 + v_{y}^2 +v_{z}^2 +v_{a}^2 .
Bei Licht ist die Geschwindigkeit in Richtung der 5. Dimension Null (v_{a} = 0), sodass der ganze Anteil von c für die Geschwindigkeit im (3-dim Beobachter-) Raum übrig bleibt. Gegenstände mit einer bestimmten Masse bewegen sich nach START auch mit c durch die 5-dim Raumzeit. Diese haben jedoch eine von Null verschiedene Geschwindigkeit in Richtung der 5. Dimension (v_{a} > 0). Da die Gesamtgeschwindigkeit immer c ist, muss der Raumanteil der Geschwindigkeit kleiner als c sein. Und da Beobachter nur das Geschehen im 3-dim Raum sehen können, bemerken sie von der zusätzlichen Bewegung in der 5. Dimension nichts. Stattdessen beobachten sie einen mit Masse behafteten Gegenstand. 

Interessant an START ist auch, dass der 3-dim Beobachterraum (x, y, z) eine ganz gewöhnliche Euklidische Metrik besitzt, d.h. auch bei Anwesenheit von Gravitation nicht gekrümmt ist. Dies erscheint uns nur so, da die wirklichen (in ihrer Gänze nicht beobachtbaren) Bahnkurven in einem 5-dim Kontinuum verlaufen.

 

Platons Höhle und die Camera obscura (dunkle Kammer)

Hier haben wir wieder unmittelbar Platons Höhle vor uns. Je nachdem wie ein höherdimensionales, lichtartiges Objekt auf die 3-dim Höhlenwand (unseren Raum) trifft (herunter projiziert wird), sehen wir dieses entweder als einen mit Masse behafteten Gegenstand oder als masseloses, auf 3 Dimensionen reduziertes Licht, d.h. als unterschiedliche Schatten einer höherdimensionalen Realität.

So ergiebig die Gravitationsgleichungen der Allgemeinen Relativitätstheorie für die Beschreibung der Gravitation und überhaupt für die ganze Kosmologie sind, bleiben sie doch in gewissem Sinne an der Oberfläche. Sie wissen nichts von einer Materie als 5. Dimension und einer Zeit, die Geschichte ermöglicht und durch eine zusätzliche 6. Dimension darstellbar ist. Natürlich kennt die Physik höhere Dimensionen, allein die Stringtheorie arbeitet mit 10 Raumdimensionen und einer Zeitdimension. Nur müssen es die „richtigen“ Dimensionen sein, um in das Innere des „globus intellectualis“ zu gelangen. Und das sind die Dimensionen eines Projektiven Raumes.

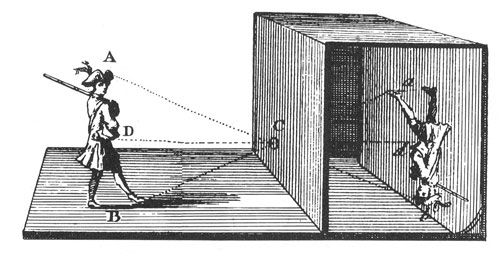
Eine Camera obscura (auch Lochkamera genannt). Der Punkt A des abzubildenden Objektes sendet zunächst Lichtstrahlen in alle Richtungen aus (ebenso jeder andere Punkt wie B oder D). Aber nur die Lichtstrahlen in Richtung C (dem focus imaginarius) gelangen ins Innere der Camera und werfen (projizieren) zusammen ein auf dem Kopf stehendes Bild auf die Rückwand. Da von den ursprünglich sehr vielen ausgehenden Strahlen pro Objektpunkt nur sehr wenige durch das möglichst kleine Loch C in der Vorderwand gelangen, ist das Abbild relativ lichtarm. Ein größeres Loch ließe zwar mehr Licht hindurch, würde aber auf Kosten der Bildschärfe gehen. (Bild: Wikipedia)

Sind die metrischen Räume (ob es nun der 4-dim oder 5-dim Minkowski Raum ist) nur die Projektionsleinwände, auf die projiziert wird, so stellt der Übergang zu einem Projektiven Raum die Vervollständigung dieser zu einer Camera obscura dar, einer kompletten Filmbühne (Kino von griech. kínēsis, Bewegung), wo das Drama des Lebens und der Evolution aufgeführt wird, wo wir Zuschauer und Akteure zugleich sind. Zur Projektionsleinwand (der Rückwand einer Camera obscura und dem Ort der Physik) kommt jetzt ein focus imaginarius (Seh- und Projektionspunkt) hinzu (das Koordinatenzentrum), in dem alle Seh- und Projektionsstrahlen gebündelt werden und der in der Vorderwand (diese entspricht dem projektiven Lichtkegel als ein Horizont) einer solchen Camera obscura liegt.

Der Kosmos offenbart sich so als ein übergeordnetes System universeller Perspektiven und Projektionen (ganz im Sinne Platons oder Leibniz’), an dem wir als endliche Wesen in unterschiedlichen Graden partizipieren, d.h. teilhaben.

 

Globus intellectualis

Der „globus intellectualis“ ist eine auf Francis Bacon zurückgehende Metapher, in der die verschiedenen Wissensgebiete der Menschheit mit den großen Landmassen (Kontinenten) der Erde verglichen werden.  Jedes Wissensgebiet hat dabei seinen eigenen Standpunkt und Horizont. Es ist der Versuch, das gesamte menschliche Wissen nach seinen verschiedenen Richtungen und Gegenständen als ein geordnetes System darzustellen.

Novum_organum_scientiarum_Bacon
Das „Novum organum scientiarum“ (dt. Neues Werkzeug der Wissenschaften) ist das 1620 in England veröffentlichte wissenschaftstheoretische, philosophische Hauptwerk von Francis Bacon. Es gilt als Wendepunkt zwischen mittelalterlichem Denken und neuzeitlicher, methodischer Forschung. Das Titelbild „Fahrt ins offene Meer“ steht programmatisch für sein „Neues Organon“ der Wissenschaft. Die Seefahrt, mit dem Ziel neue Länder zu entdecken, wird metaphorisch zur Wissensexpedition. Francis Bacon: „Nachdem ich so an den alten Küsten vorübergesegelt bin, werde ich den menschlichen Geist zur Fahrt ins offene Meer vorbereiten.“ (Bild: Wikipedia)

Auch Kant greift darauf zurück, um seine Transzendental-Philosophie zu veranschaulichen. Die Oberfläche des „globus intellectualis“ bilden dabei wieder die Erfahrungswissenschaften (Tatsachen- oder Naturwissenschaften). Für Kant gibt es aber ausgezeichnete Perspektiven, die ins Innere des Globus führen und die Wege der Philosophie sind. Im Zentrum befindet sich, der äußeren Sonne gleich, um die sich alle Planeten drehen, eine innere Sonne: ein übergeordneter Standpunkt, der die verschiedenen Perspektiven der Erfahrungswissenschaften auf der Oberfläche überhaupt erst ermöglicht, beleuchtet und zu einer höheren Einheit verbindet.

Andere Philosophen haben ebenfalls diese Metapher (in leicht abgewandelter Form) verwendet. Paul Natorp (dt. Philosoph, 1854-1924), der zusammen mit Hermann Cohen (dt. Philosoph, 1842-1918), Mitbegründer der Marburger Schule des Neukantianismus ist, stellt z.B. die Beziehung der Tatsachenwissenschaften zur Philosophie anhand einer Kreismetapher dar:

„[…] der Weg gleichsam zum Zentrum: der Einheit der Erkenntnis, und zum Umkreis: der unbegrenzbaren Mannigfaltigkeit der besonderen und einzelnen Erkenntnisse. Wie also die Wege von der Peripherie zum Zentrum und vom Zentrum zur Peripherie der Richtung nach einander entgegengesetzt, dabei aber doch eins sind, indem alle und nur dieselben Punkte in einer und der anderen Richtung durchlaufen werden müssen, so verhalten sich zueinander, ideal genommen, die Wissenschaften und die Philosophie.“

Weitere Metaphern neben dem “Zentrum des Kreises” nach Cohen sind:  der „Logos selbst“ nach Platon und die „synthetische Einheit der transzendentalen Apperzeption“ nach Kant.

 

* Genaugenommen müsste die Wirkungsdichte a noch mit einer entsprechenden Konstanten multipliziert werden, damit diese ebenfalls, wie x, y, z, eine Länge ist. Aber auf solche Feinheiten soll hier zwecks der Übersichtlichkeit verzichtet werden. t steht für ct mit c = 1.