Der Mensch der Frühzeit machte zwei für sein Weltverständnis entscheidende Beobachtungen:
1. Alles in seiner Umgebung schien ihm wie mit einem magischen Bann belegt. Pflanzen, Tiere und auch er selbst waren einem zwar langsamen, aber dafür stetigen Wandel unterworfen. Dinge entstanden neu, wurden geboren, wuchsen heran, existierten eine Zeit lang und verschwanden wieder. Mutter Natur brachte alles Leben hervor, nährte ihre Kinder und nahm sie dann eines Tages wieder zu sich.
2. Ganz anders waren ihm die Erscheinungen am Himmel. Bei Tage war es die Sonne, ohne deren Licht erst gar kein Leben existieren konnte, und bei Nacht der Mond und die Sterne. Die Gestirne waren scheinbar keinem Wandel unterworfen und in immer gleichen Bahnen zogen sie über das Himmelsgewölbe. Sie waren den frühen Menschen nicht nur ein Sinnbild für das Unvergängliche, sondern sichtbare Manifestation höherer Mächte.
Der Kosmos wurde hierarchisch geordnet. Oben am Himmelsfirmament thronten die Götter und unten auf Erden wandelte der vergängliche Mensch. Durch das Studium der Planetenbahnen glaubte man auch, die Zukunft vorhersagen und auf das Schicksal Einfluss nehmen zu können.

Stonehenge, ein Observatorium aus der Jungsteinzeit. Credit & Copyright: Max Alexander, STFC, SPL
Sein und Werden
Wie sehr sich das Bild von einem ewigen und immer gleichbleibenden Universum seither im Denken verankert hat, zeigt das Beispiel Albert Einstein (1879-1955, dt. Physiker). Als seine Allgemeine Relativitätstheorie kein statisches, sondern ein dynamisches Universum vorhersagte, glaubte er zunächst an einen Fehler der Feldgleichung und korrigierte sie um eine Kosmologische Konstante. Durch die Analyse des Lichts ferner Sterne zeigte sich jedoch, dass das Universum tatsächlich expandiert, und Einstein nahm seine Korrektur wieder zurück.
Die ganze Philosophiegeschichte ist von diesem Spannungsfeld zwischen Ewigem und Vergänglichem, Absolutem und Relativem durchzogen und in den modernen Wissenschaften nur im neuen Gewande wieder auferstanden.
Diese Suche des Menschen nach dem Ewigen und Absoluten hat im Laufe der Geschichte viele unterschiedliche Metamorphosen erfahren. Mal waren es Götter, dann wieder ein Urstoff, aus dem alles entsteht:
Bei Parmenides von Elea (540/535 – 483/475 v. Chr., gr. Philosoph) wird es zum ersten Mal ganz abstrakt als Sein formuliert. Es ist eine ungeschaffene, unveränderliche, unzerstörbare Einheit, und allein ihr kommt Realität zu. Im Gegensatz dazu hat die sich in der Alltagswahrnehmung zeigende, sich in ständigem Wandel befindliche Vielheit keine eigene Realität. Alles Werden, alle Bewegung, alle Vielheit ist nur Schein.
Dem widerspricht Heraklit von Ephesos (um 520-460 v. Chr., gr. Philosoph) und für ihn ist das Grundprinzip des Kosmos nicht ein statisches, gleichbleibendes Sein, sondern das Werden. Polarität bringt Bewegung und Veränderung hervor, die durch den Logos, das ewige Weltfeuer, harmonisiert wird.
Platon (428/427-348/347 v. Chr., gr. Philosoph) versucht die (von ihm etwas stilisierte) Streitfrage zwischen Parmenides und Heraklit, was denn nun wichtiger wäre bzw. wem mehr Realität zukommt, dem Sein oder dem Werden, durch ein eigenes philosophisches System zu beantworten. Platon ersetzt das Sein des Parmenides durch die Platonischen Ideen, die für ihn ebenfalls höchste Realität sind. Die geschaffenen, vergänglichen Dinge sind jetzt aber durch Teilhabe (gr. methexis) mit den Ideen verbunden. Das gibt ihnen eine gewisse, wenn auch abgeschwächte Realität. Da „Alles Sinnliche will sein wie die Idee“ (Phaidon), entsteht Bewegung und Veränderung.
In der Frage, wem nun mehr Realität zukommt, dem Sein oder dem Werden, schlägt sich Platon also eher auf die Seite des Parmenides. Er spricht den geschaffenen Dingen aber wenigstens etwas Realität zu. Aristoteles (384-322 v. Chr., gr. Philosoph) hingegen lenkt die Aufmerksamkeit wieder mehr auf die Materie und ihre Wandlungen und steht damit Heraklit näher.
Wer nun annimmt, dass dieses alte Thema vom Sein und Werden nur ein aus der antiken Philosophie übrig gebliebenes Relikt ist, das uns heute nicht mehr viel zu sagen hat, irrt.
Ersetzt man nämlich Sein durch Invariante (unveränderliche Größe) und Werden durch Transformation, befinden wir uns mit einem Schlag im 19. Jahrhundert und mitten im Erlanger Programm von Felix Klein. Es wird sich zeigen, dass weder dem Sein noch dem Werden der Vorzug gebührt, sondern beide untrennbar miteinander verbunden sind.
Das Erlanger Programm
Über 2000 Jahre lang galt die Euklidische Geometrie als einzig mögliches geometrisches System. Im 17. Jahrhundert erwachte die Mathematik dann aus ihrem Dornröschenschlaf und in ihrem rasanten Vorwärtsschreiten zerfiel sie in immer mehr hoch spezialisierte Teilgebiete.
Neben der Euklidischen Geometrie gab es plötzlich die Projektive Geometrie, die Hyperbolische Geometrie und die Elliptische Geometrie. Die Mathematik wurde langsam aber sicher unübersichtlich und es fehlte ihr an einem einheitlichen Ordnungsschema.
Die Euklidische Geometrie ist die Geometrie der Ebene und hat die Krümmung Null. Die Hyperbolische Geometrie ist die Geometrie auf einer Sattelfläche und hat ein konstantes negatives Krümmungsmaß. Die Elliptische Geometrie ist die Geometrie auf einer Kugeloberfläche und besitzt ein konstantes positives Krümmungsmaß.
Indem Bernhard Riemann (1826-1866, dt. Mathematiker) zeigte, dass die Euklidische, die Hyperbolische und die Elliptische Geometrie nur Spezialfälle höherdimensionaler Räume mit beliebig variabler Krümmung sind, gelang ihm zwar eine gewisse Vereinheitlichung, aber er erfasste damit nur Geometrien mit einer metrischen Struktur (in denen man Längen und Winkel messen kann). Projektive oder Topologische Räume z.B. wurden durch dieses horizontale Ordnungsschema nicht erfasst.
Es ist das Verdienst von Felix Klein (1849-1925, dt. Mathematiker), eine Methode gefunden zu haben, mit der sich Geometrien auch vertikal klassifizieren, d.h. über- und unterordnen lassen. Mit Hilfe des Erlanger Programms ist es möglich, geometrische Strukturen durch eine vertikale Hierarchie zu ordnen. Wie in der Ideenpyramide Platons steigt man darin vom Besonderen und Konkreten zum Allgemeinen und Abstrakten auf.

Felix Klein (1849-1925) war ein deutscher Mathematiker und begründete das Erlanger Programm
Dieses hierarchische Ordnungsschema für geometrische Strukturen lässt sich auch auf die Natur und den gesamten Kosmos übertragen. Man muss sich nur der Worte Galileo Galileis (1564-1642, ital. Naturforscher) aus seinem Buch „Il Saggiatore“ (Die Goldwaage) erinnern:
„Das Buch der Natur ist in der Sprache der Mathematik geschrieben und ihre Buchstaben sind Dreiecke, Kreise und andere geometrische Figuren, ohne die es ganz unmöglich ist auch nur einen Satz zu verstehen, ohne die man sich in einem dunklen Labyrinth verliert“.
Für Isaac Newton (1642-1727, engl. Naturforscher) war der Physikalische Raum noch dreidimensional und Euklidisch. Unter Hermann Minkowski (1864-1909, dt. Mathematiker), der Einsteins Spezielle Relativitätstheorie geometrisch deutete, verwandelte sich der Newtonsche Raum in das vierdimensionale Raumzeit-Kontinuum mit Pseudoeuklidischer Metrik. Auf einer noch höheren Abstraktionsebene, der Twistor-Theorie, verlieren sogar Raum und Zeit ihre fundamentale Bedeutung, und an ihre Stelle tritt eine Art Lichtraum, ein dreidimensionaler Projektiver Raum mit komplexwertigen Koordinaten.
Dieses hier nur ganz grob skizzierte Aufsteigen zu immer höheren und abstrakteren Räumen lässt sich im hierarchischen Ordnungsschema von Felix Klein genau verfolgen. Die ganze Suche nach einer „Weltformel“ entspricht einer solchen Aufwärtsbewegung zu immer höheren und abstrakteren hierarchischen Ebenen. Was wird ganz oben auf der Spitze dieser Stufenpyramide als höchstes allumfassendes Prinzip stehen? Die Platonische Sonne, in der alles Sein und Werden seinen Ursprung hat?
Aber zunächst zurück zum Fundament der Pyramide und beginnen wir mit einem etwas langsameren Aufstieg. Wird der Weg vielleicht auch manchmal nicht ganz einfach sein, so lohnt es sich doch, ihn bis zum Ende zu gehen. Selbst Fragen nach dem Verhältnis von Subjekt und Objekt, was Bewusstsein, was Materie eigentlich ist, können auf dem Weg zur Pyramidenspitze aus einem ganz neuen Blickwinkel betrachtet werden, und vielleicht gelingt es uns sogar, befriedigende Antworten darauf zu geben.
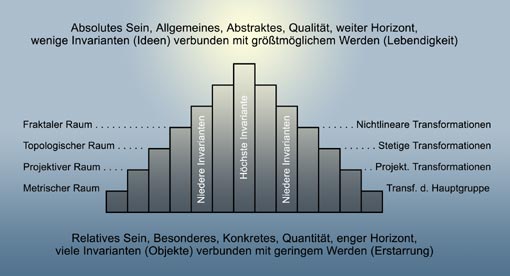
Pyramide vom Sein und Werden: Die Stufen der Pyramide versinnbildlichen die durch die Transformationsgruppen festgelegte hierarchische Ordnung. Am Fuße der Pyramide existieren die meisten Invarianten und sie verkörpern die sichtbare Welt. Je höher wir die Pyramide hinaufsteigen, umso geringer wird die Anzahl der Invarianten. Sie schmelzen gleichsam dahin. Mit jeder Stufe aufwärts werden die Invarianten abstrakter und allumfassender. Ganz oben auf der Spitze gibt es dann nur noch eine einzige und letzte Invariante. Sie alleine kann den dort herrschenden alles transformierenden Kräften noch standhalten und sie alleine existiert gleichzeitig auch auf allen anderen Seinsebenen, von der Spitze bis zum Boden der Pyramide
Um nun eine Vorstellung zu bekommen, wie das Erlanger Programm von Felix Klein eigentlich funktioniert, ein einfaches Beispiel:
Zeichnet man in der Ebene einen Kreis und verschiebt ihn dann geradlinig an einen anderen Ort, wird in der Sprache der Mathematik eine ganz spezielle Transformation durchgeführt, eine so genannte Translation. Der Kreis befindet sich jetzt zwar an einer anderen Stelle, aber seine Form hat sich durch diese Transformation nicht verändert. Es ist immer noch der gleiche Kreis. Mathematisch ausgedrückt heißt das: Der Begriff Kreis ist invariant unter der Transformation namens Translation. Auch bei einer Drehung bleibt der Kreis ein Kreis. Erst durch Dehnen und Strecken (wie auf einem Gummituch) verliert der Kreis seine Form. Hinsichtlich solcher Transformationen ist der Begriff Kreis keine Invariante mehr.
Am Beispiel des Kreises zeigt sich bereits, dass der Begriff Invarianz (der eine enge Verwandtschaft mit dem Begriff Objektivität aufweist) ein relativer Begriff ist: Etwas ist invariant nur in Bezug auf bestimmte Transformationsgruppen.
Solche Transformationsgruppen haben nun die Eigenschaft, dass sie eine innere hierarchische Struktur ähnlich einem Stammbaum besitzen. Eine Gruppe beinhaltet in der Regel kleinere Gruppen, so genannte Untergruppen, und diese haben wieder kleinere Untergruppen. Umgekehrt kann man zu immer umfangreicheren Transformationsgruppen hinaufsteigen. So sind die Translationen und Drehungen in der Euklidischen Geometrie Untergruppen der Hauptgruppe, und diese wiederum ist eine Untergruppe der Projektiven Transformationen.
Felix Kleins grundlegender Gedanke besteht nun darin, Geometrien durch Transformationsgruppen zu charakterisieren. Objekte und Begriffe einer bestimmten Geometrie sind dann die Invarianten der entsprechenden Transformationsgruppe. Z.B. ist die zur Euklidischen Geometrie gehörige Transformationsgruppe die Hauptgruppe, und durch sie werden die invarianten Begriffe Kongruenz, Ähnlichkeit, Parallelität usw. bestimmt. Sowohl die Euklidische Geometrie als auch die Hyperbolische und die Elliptische Geometrie besitzen jeweils ihre eigene sie charakterisierende Transformationsgruppe. Ihnen allen Dreien ist aber gemeinsam, dass sie Untergruppe einer übergeordneten größeren Gruppe sind. Es ist dies die Gruppe der Projektiven Transformationen, die ihrerseits die Projektive Geometrie bestimmt.
Die Projektive Geometrie ist somit eine der Euklidischen und den beiden anderen nichteuklidischen Geometrien übergeordnete Geometrie, eine Art Meta-Geometrie.
Umgekehrt steigt man in der Hierarchie von der Projektiven Geometrie zu den drei einzelnen Geometrien mit ihren unterschiedlichen Krümmungsmaßen herab, indem ein so genanntes Fundamentalgebilde (Absolutfigur), ein Horizont, als eine Invariante vorgegeben wird. Ein solcher Horizont umschließt die gesamte zugehörige Geometrie gleichsam als ein Unendlichfernes. Wird als Horizont z.B. eine Gerade vorgegeben, müssen aus der Projektiven Gruppe all jene Transformationen entfernt werden, die diese Gerade (und zwei auf ihr liegende imaginäre Punkte) nicht invariant lassen. Übrig bleibt dann genau die Hauptgruppe der ebenen Euklidischen Geometrie. Wird als Horizont ein Kreis vorgegeben, sind entsprechend die Transformationen aus der Projektiven Gruppe wegzulassen, welche die Invarianz dieses Horizontkreises zerstören. Die so reduzierte Transformationsgruppe bestimmt dann die Hyperbolische Geometrie. Die Elliptische Geometrie besitzt einen imaginären Horizont.
Durch die spezielle Wahl eines Fundamentalgebildes als Horizont und die Forderung seiner Invarianz wird innerhalb der Gruppe der Projektiven Transformationen genau eine Untergruppe bestimmt, welche ihrerseits die entsprechende Metrische Geometrie festlegt.

Kreislimit IV von M. C. Escher (1898-1972). Das Bild zeigt die Geometrie eines Hyperbolischen Universums. Obwohl dieses Universum von außen betrachtet begrenzt erscheint ist es für seine Bewohner unendlich groß, da durch die Metrik der Hyperbolischen Geometrie der Abstand von einem beliebigen Punkt innerhalb des Kreises bis zum Kreisrand immer unendlich groß ist. Für einen außenstehenden Beobachter wird ein Bewohner dieser Welt, der sich dem Rand seines Universums mit gleichbleibender Geschwindigkeit zu nähern versucht, immer kleiner und langsamer, so dass er den Rand des Kreises, den Horizont, nie erreicht. Im Bild ist das durch die zum Rand hin kleiner werdenden „Engelchen und Teufelchen“ angedeutet
Das Universum hat auf genügend großen Skalen eine – von seiner mittleren Materiedichte abhängige – konstante Raumkrümmung. Ähnlich wie für einen Beobachter durch die Erdkrümmung ein Horizont entsteht, hat auch das Universum einen mit seiner Raumkrümmung korrespondierenden Horizont.
Die Frage, ob diese mittlere Raumkrümmung des Universums nun null (Euklidischer Raum), negativ (Hyperbolischer Raum) oder positiv (Elliptischer Raum) ist, mögen vielleicht viele nicht als besonders wichtig erachten, selbst wenn davon abhängt, ob das Universum für immer expandiert oder eines Tages wieder zu einem Punkt kollabiert. Ebenso wird die Tatsache, dass die Geometrie des Universums statt durch eine mittlere Krümmung auch durch die Form seines Horizonts beschrieben werden kann, wohl bei den Wenigsten großes Staunen auslösen. Aber dass das Universum als Ganzes überhaupt so etwas wie einen ihn begrenzenden Horizont besitzt, sollte zumindest aufhorchen lassen, stellt sich doch die Frage: „Was liegt hinter dem Horizont und wessen Horizont ist das?“
Was es mit diesem das Universum umschließenden, unendlich fernen Horizont genauer auf sich hat, und wie er unseren „Blick auf die Welt“ verändern kann, wird sich in den Fortsetzungen zeigen.
Zur Fortsetzung: Horizonte 3 〉〉〉