Horizonte 9 – Teil B (Takimo 31)

II. Felix Klein:

Zunächst eine Zusammenstellung, wie sich die verschiedenen Räume der Physik aus Sicht des Erlanger Programms mithilfe der Projektiven Geometrie und eines ausgezeichneten projektiven Lichtkegels (Fundamentalgebilde, Absolutfigur, Horizont) in einem 5-dim Projektiven Raum darstellen und systematisieren lassen.

1. Die Newton Raum-Zeit ist durch die Galilei-Transformationen bestimmt. Der projektive Lichtkegel lautet:

X_1^2+X_2^2+X_3^2 = 0  und X_4 = 0 und X_5 = 0 (zweifach entartet)

Die Invariantentheorie bzgl. der Galilei-Transformationen wird auf der durch X_5 = \textnormal{const} := 1 gegebenen 4-dim Mannigfaltigkeit konstruiert und ist die Raum-Zeit der Klassischen Mechanik.

2. Die Minkowski Raumzeit ist durch die Poincaré-Transformationen (inhomogene Lorentz-Transformationen) bestimmt. Der projektive Lichtkegel lautet:

X_1^2 + X_2^2 + X_3^2 - X_4^2 = 0 und X_5 = 0 (einfach entartet)

Die Invariantentheorie bzgl. der Poincaré-Transformationen wird auf der durch X_5 = \textnormal{const} := 1 gegebenen 4-dim Mannigfaltigkeit konstruiert und ist die Raumzeit der Speziellen Relativitätstheorie.

3. Die deSitter Raumzeit hat den projektiven Lichtkegel:

X_1^2 + X_2^2 + X_3^2 - X_4^2 + X_5^2 = 0

Die entsprechende Physik wird jetzt nicht auf der durch X_5 = 1 gegebenen Mannigfaltigkeit (wie in der Newton und Minkowski Raumzeit) konstruiert, sondern mittels des Hyperboloids

X_1^2 + X_2^2 + X_3^2 - X_4^2 + X_5^2 = \frac{3 }{\Lambda}, dem deSitter Universum, mit der Kosmologischen Konstante \Lambda .

Höhersymmetrische Lösungen für die Einsteinschen Gravitationsgleichungen lassen sich finden, wenn der Hyperboloid des deSitter Universums nicht in einem 5-dim, sondern 6-dim Projektiven Raum, wie folgt, eingebetet wird:

1. Möglichkeit: Der die Metrik einer Geometrie erzeugende projektive Lichtkegel ist nun

X_1^2 + X_2^2 + X_3^2 - X_4^2 + X_5^2 = 0 und X_6 = 0 (einfach entartet)

Konstruiert wird die Invariantentheorie auf der durch X_6 := 1 festgelegten 5-dim Mannigfaltigkeit. Die sich daraus ergebende metrische Geometrie ist wieder eine flache Minkowski Raumzeit, nur diesmal mit 4 statt 3 räumlichen Dimensionen. Hatte die Minkowski Raumzeit die orthogonalen Transformationen O(1,3), die Lorentz-Transformationen, als Symmetriegruppe, so sind es jetzt die orthogonalen Transformationen der Symmetriegruppe O(1,4).

Das deSitter Universum, die 4-dim Oberfläche des Hyperboloids, ist jetzt eingebettet in eine 5-dim Minkowski Raumzeit.

2. Möglichkeit: Ist der projektive Lichtkegel

X_1^2 + X_2^2 + X_3^2 - X_4^2 + X_5^2 - X_6^2 = 0 und schneiden wir diesen mit der Ebene X_6 := 1 , dann ist die Schnittfigur X_1^2 + X_2^2 + X_3^2 - X_4^2 + X_5^2 - 1 = 0 bzw. X_1^2 + X_2^2 + X_3^2 - X_4^2 + X_5^2 = 1 . Das ist aber wieder das deSitter Universum in projektiven Koordinaten. Nur existiert jetzt dieses Universum auf dem die Geometrie bestimmenden projektiven Lichtkegel selbst und hat als Symmetriegruppe die Konformen-Transformationen. Diese Transformationen (und die damit verbundenen Beobachterperspektiven) bestehen aus 3 Drehungen im Raume, 3 gleichförmigen Geschwindigkeiten (in die verschiedenen Raumrichtungen), 3 Translationen im Raum und 1 in der Zeit (das sind zusammen die 10 Parameter der Poincaré-Transformationen) und noch 5 weiteren Parametern: 1 für Streckungen (Dilatationen, die die Metrik um eine glatte Funktion skalieren) und 4 für Transformationen durch reziproke Radien, das sind Inversionen (Spiegelungen) an Kugeloberflächen. Macht zusammen 15 Parameter. Die zugehörige Symmetriegruppe ist O(2,4). Das O steht wieder für orthogonale Transformationen und (2,4) bedeutet, dass diese Raumzeit 2 zeitliche und 4 räumliche Dimensionen besitzt. Mit dieser zusätzlichen Zeit- und Raumdimension werden wir uns schon bald ausgiebiger beschäftigen, aber zunächst sollen noch die Betrachtungen über das deSitter Universum abgeschlossen werden.

 

Die Physik des deSitter Universums

Wir kehren zu dem vorangegangenen Fall (1. Möglichkeit) zurück, wo die deSitter Mannigfaltigkeit X_1^2 + X_2^2 + X_3^2 - X_4^2 + X_5^2 = \frac{3 }{\Lambda} in eine 5-dim Minkowski Raumzeit mit der Symmetriegruppe O(1,4) und dem metrischen Fundamentaltensor G_{ij} = \mathrm{diag}(1, 1, 1, -1, 1) eingebettet ist. Um herauszufinden, welche Physik auf der deSitter Mannigfaltigkeit möglich ist, muss die entsprechende Metrik auf dem Hyperboloid berechnet werden. Diese ist bestimmt durch die Metrik der umgebenden Raumzeit und welche Koordinaten auf dem Hyperboloid eingeführt werden. Die Formel dazu lautet:

g_{ \mu \nu} = \frac{\partial X^i }{\partial x^\mu} \frac{\partial X^j }{\partial x^\nu}G_{ij}

G_{ij} ist die Metrik des Umgebungsraumes und die Substitution X^i = X^i (x, y, z, t) oder allgemeiner = X^i (\varphi, \theta, \chi, t) entspricht einer Koordinaten-Transformation.

Der Zweck einer solchen Einführung krummliniger Koordinaten lässt sich am Beispiel der Erde deutlich machen. So, wie jeder Punkt der Eroberfläche vom Zentrum gleichweit entfernt ist ( X_1^2 + X_2^2 + X_3^2 = R^2, R ist der Erdradius), ist auch jeder Punkt des deSitter Universums vom Koordinaten-Zentrum der umgebenden Raumzeit gleichweit entfernt, nämlich \sqrt{\frac{3 }{\Lambda}} .
Um z.B. den Abstand von der Erde zum Mond zu messen, wird man einfach eine (euklidische) Gerade ziehen. Um aber Abstände auf der gekrümmten Eroberfläche zu messen, muss eine andere Maßbestimmung eingeführt werden, eine elliptische Metrik. Geometrisch gesehen wird der Abstand zwischen 2 Punkten auf der Erdoberfläche dadurch gemessen, dass die von den 2 Punkten und dem Erdmittelpunkt aufgespannte Ebene mit der Kugeloberfläche geschnitten wird. Die Länge der dabei entstehenden Schnittfigur, ein Kreisbogen, gibt dann den entsprechenden Abstand an. Sinnvollerweise werden auf der Erdoberfläche für Ortsangaben und das Messen von Abständen sogenannte Kugelkoordinaten eingeführt. 

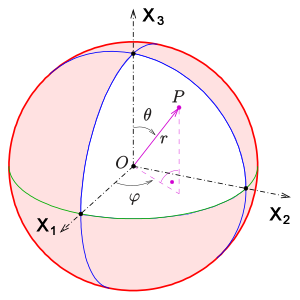
Kugelkoordinaten

In Kugelkoordinaten wird ein Punkt des Raums durch seinen Abstand vom Ursprung und durch zwei Winkel angegeben. Koordinatenlinien erhält man, indem jeweils zwei Koordinaten festgehalten und die dritte variiert wird. Solche Koordinatenlinien entstehen auch durch den Schnitt der Kugeloberfläche mit entsprechenden Ebenen. (Bild: Wikipedia)

Es gilt:

X_1(\varphi, \theta, r) = r \sin(\theta) \cos(\varphi)

X_2(\varphi, \theta, r) = r \sin(\theta) \sin(\varphi)

X_3(\varphi, \theta, r) = r \cos(\theta)

mit \varphi im Intervall [0, 2\pi] und \theta im Intervall [0, \pi]

Für eine Kugel, eingebettet in einem Euklidischen Raum, G_{ij} = \mathrm{diag}(1, 1, 1), berechnet sich mit der Formel g_{ \mu \nu} = \frac{\partial X^i }{\partial x^\mu} \frac{\partial X^j }{\partial x^\nu}G_{ij} die g_{ \mu \nu} und damit das Linienelement (infinitesimales Wegelement) in Kugelkoordinaten 

\mathrm{d}s^2 = \mathrm{d}X_1^2 + \mathrm{d}X_2^2 + \mathrm{d}X_3^2 = g_{11} \mathrm{d}r^2 + g_{22} \mathrm{d}\theta^2 + g_{33} \mathrm{d}\varphi^2 = \mathrm{d}r^2 + r^2 \mathrm{d}\theta^2 + r^2 \sin^2(\theta)\mathrm{d}\varphi^2

Auf der Kugeloberfläche gilt r = R (const) und damit \mathrm{d}r = 0 und
\mathrm{d}s^2 = R^2 \mathrm{d}\theta^2 + R^2 \sin^2(\theta) \mathrm{d}\varphi^2

Ganz analog ist das Vorgehen im Fall des deSitter Universums. Je nach Koordinatenwahl erhält man unterschiedliche Lösungen der Einsteinschen Gravitationsgleichungen und zwar (mit c = 1):

 

A. Ein räumlich flaches deSitter Universum

X_i = X_{i}(x, y, z, t) mit i=1,2,3,4,5 und H = \sqrt{\frac{\Lambda }{3}} ist der Hubble-Parameter

X_1 = e^{Ht} x  

X_2 = e^{Ht} y  

X_3 = e^{Ht} z  

X_4 = \frac{1}{H} \sinh(Ht) + \frac{H}{2} e^{Ht} (x^2 + y^2 + z^2)  

X_5 = \frac{1}{H} \cosh(Ht) - \frac{H}{2} e^{Ht} (x^2 + y^2 + z^2)  

Für das Linienelement ergibt sich
\mathrm{d}s^2 = \mathrm{d}t^2 - e^{2Ht} (\mathrm{d}x^2 + \mathrm{d}y^2 + \mathrm{d}z^2)
Die gewählten Koordinaten beschreiben einen flachen, um den Faktor e^{2Ht} exponentiell expandierenden Raum. Für \Lambda = 0 und damit H = 0, gilt
\mathrm{d}s^2 = \mathrm{d}t^2 - \mathrm{d}x^2 - \mathrm{d}y^2 - \mathrm{d}z^2
Das aber ist wieder das Linienelement der Minkowski Raumzeit in 4 Dimensionen.

 

B. Ein räumlich geschlossenes deSitter Universum

X_i = X_{i}(\varphi, \theta, \chi, t) bzw.

X_1 = \frac{1}{H} \cosh(Ht) \cos\chi

X_2 = \frac{1}{H} \cosh(Ht) \sin(\chi) \cos(\theta)

X_3 = \frac{1}{H} \cosh(Ht) \sin(\chi) \sin(\theta) \cos(\varphi)

X_4 = \frac{1}{H} \sinh(Ht)

X_5 = \frac{1}{H} \cosh(Ht) \sin(\chi) \sin(\theta) \sin(\varphi)

Das Linienelement ist in diesem Fall
\mathrm{d}s^2 = \mathrm{d}t^2 - \frac{1}{H^2}\cosh^2(Ht) (\mathrm{d}\chi^2 + \sin^2(\chi) (\mathrm{d}\theta^2 + \sin^2(\theta) \mathrm{d}\varphi^2))
In diesen Koordinaten sieht der deSitter Raum aus wie eine 3-Sphäre mit positiver Krümmung, der bei t = 0 minimale Ausdehnung hat und dann mit wachsender Zeit t exponentiell zu unendlicher Größe expandiert.

 

C. Ein räumlich offnes deSitter Universum

X_1 = \frac{1}{H} \cosh(Ht)

X_2 =\frac{1}{H} \sinh(Ht) \sinh(\chi) \cos(\theta)

X_3 = \frac{1}{H} \sinh(Ht) \sinh(\chi) \sin(\theta) \cos(\varphi)

X_4 = \frac{1}{H} \sinh(Ht) \cosh(\chi)

X_5 = \frac{1}{H} \sinh(Ht) \sinh(\chi) \sin(\theta) \sin(\varphi)

In diesen Koordinaten ist
\mathrm{d}s^2 = \mathrm{d}t^2 - \frac{1}{H^2} \sinh^2(Ht) (\mathrm{d}\chi^2 + \sinh^2(\chi)(\mathrm{d}\theta^2 + \sin^2(\theta) \mathrm{d}\varphi^2
Damit gleicht der deSitter Raum einem 3-Hyperboloid mit negativer Krümmung. 

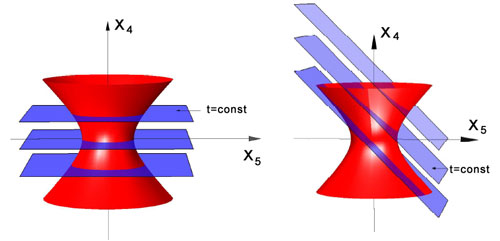
Schnitte_Hyperboloid

Links: Das räumlich geschlossene deSitter Universum. Die Schnittfiguren der blauen Ebenen (feste Zeiten t und X_4 = \frac{1}{H} \sinh(Ht)) mit dem roten Hyperboloid ergeben 3-Sphären. 
Rechts: Das räumlich flache deSitter Universum. Die Schnittfiguren der blauen Ebenen (feste Zeiten t und X_4 + X_5 = \frac{1}{H}e^{Ht}) mit dem roten Hyperboloid ergeben flache 3-dim Räume. 

 

Eine kurze Zusammenfassung und Ausblick:

Die Einsteinschen Gravitationsgleichungen der Allgemeinen Relativitätstheorie haben von Anfang an 3 Raum- und 1 Zeitkoordinate (x, y, z, t) und die Metrik ist durch 10 metrische Koeffizienten g_{ \mu \nu} (mit g_{ \mu \nu} = g_{ \nu \mu} und i, j = 1,2,3,4) als Lösungen von Differentialgleichungen bestimmt.

Die projektive Betrachtung (nach dem Erlanger Programm) arbeitet zunächst mit 5 oder 6 homogenen Koordinaten (X_1, X_2, X_3, X_4, X_5, X_6) := (X_i). Homogene Koordinaten bedeutet (X_i) = \lambda (X_i) = (\lambda X_i). Mithilfe eines projektiven Lichtkegels wird dann auf einer entsprechenden Mannigfaltigkeit die Invariantentheorie (Metrik) mit den zugehörigen inhomogenen (und damit physikalischen) Koordinaten (x, y, z, t) entwickelt. Während homogene Koordinaten Geraden durch das Koordinatenzentrum des Projektiven Raumes entsprechen, können inhomogene Koordinaten eindeutig einem Punkt zugeordnet werden.

Das START Konzept von Jaime Keller arbeitet mit 3 Raum-, 1 Zeit- und 1 „Materie“-Koordinate (x, y, z, t, a) in einer 5-dim Minkowski Raumzeit mit G_{ij} = \mathrm{diag} (1, 1, 1, -1, 1). Die Physik wird dabei auf der durch a = a(x, y, z, t) gegebenen Mannigfaltigkeit konstruiert. START nimmt dabei keinen direkten Bezug auf den projektiven Hintergrund. Das muss es als ein nur auf die Physik beschränktes einheitliches Konstruktionsprinzip auch nicht. Für uns, die wir in das Innere des „globus intellectualis“ wollen, ist dies aber von großer Bedeutung. Dazu in den nächsten Lexikonpunkten mehr. 

Zur Fortsetzung:   Horizonte 9 – Teil C   〉〉〉