Kant untersucht in der Kritik der reinen Vernunft (KdrV) die Struktur des erkennenden Bewusstseins. Eine zentrale Frage dabei lautet: “Wie sind synthetische Urteile a priori möglich?” Das heißt: Wie kann sich unser Bewusstsein aus sich selbst heraus erweitern, Erkenntnisse gewinnen, ohne vorausgehende empirische Erfahrungen gemacht zu haben? Das Paradebeispiel dafür ist die Mathematik.
Ermöglicht wird dies nach Kant durch die Einheit stiftende Kraft der transzendentalen Apperzeption, des “Ich bin”. Das heißt, in der Mathematik untersucht das Bewusstsein sich selbst und legt seine Struktur in Form von Mathematik offen. Nun ist Mathematik zugleich die Sprache der Naturwissenschaften, speziell der Physik, und es stellt sich die Frage, wie menschliche Bewusstseins-Strukturen so exakt auf die Welt der Materie passen. Was für Physiker ein großes Rätsel darstellt (mit dem sie sich aber kaum bis gar nicht beschäftigen, Hauptsache der mathematische Formalismus funktioniert), ist für Kant eine klare Sache: Die Außenwelt, welche wir wahrnehmen, ist die Welt der Erscheinungen (Phänomene). Das heißt, beginnend von den ersten Empfindungen durch die Sinne (Perzeptionen), bis hin zur begrifflichen Verarbeitung im Verstande, spielt sich alles in unserem Bewusstsein ab. Was die “Dinge an sich selbst” sind, also unabhängig von unserem Bewusstsein, können wir nicht wissen. Denn von Dingen können wir nur etwas wissen, wenn sie gerade als eine Vorstellung in unserem Bewusstsein sind, oder zumindest schon einmal waren und im Gedächtnis aufbewahrt werden.
Die sogenannte Objektivität der Naturwissenschaft kommt nun dadurch zustande, dass die zunächst noch rohe Empfindungs-Materie mittels universeller Strukturen des Bewusstseins, den Anschauungs- und Denkformen, geordnet wird. Die so den einzelnen Vorstellungen aufgeprägte universelle Struktur wird dann anschließend wieder nach außen projiziert, wo die Naturwissenschaft sie als objektive Gegenstände klassifiziert.
Hier ist der Ort großer Verständnisschwierigkeiten und zahlreicher Fehlinterpretationen Kantischer Transzendental-Philosophie. Raum ist auf der Ebene der sinnlichen Anschauung “Anschauungsform des äußeren Sinnes” und Zeit “Anschauungsform des inneren Sinnes”. Raum als eine Anschauungsform des äußeren Sinnes ist eine universelle Bewusstseinsstruktur, die es einem Ich ermöglicht, Dinge “scheinbar außer sich” im Raume anzuschauen. “Scheinbar außer sich” deshalb, weil diese Art von Raum zum Bewusstsein des Ichs gehört und vielmehr ein Bewusstseins-Raum ist, der zunächst nichts mit irgendeinem physikalischen Raum, sei er nun gekrümmt oder nicht, zu tun hat. Geometrische und physikalische Räume entstehen erst, wenn geometrische und physikalische Begriffe auf der Verstandesebene in diesem Bewusstseins-Raum der äußeren Anschauung durch Konstruktion dargestellt werden. Für Kant ist der Raum zugleich “empirisch real und transzendental ideal” (KdrV). Darum macht es keinen Unterschied zu sagen: Die Dinge sind im Raum oder die Dinge sind im Bewusstsein.
Diesen Bewusstseins-Raum der äußeren Anschauung und die Bewusstseins-Zeit der inneren Anschauung (darin sich ein Ich selbst anschaut) mit Hilfe mathematischer Strukturen darzustellen und ihren Zusammenhang mit den Räumen der Physik aufzuzeigen, soll Ziel der weiteren Betrachtung sein. Wir begeben uns sozusagen auf die Suche nach dem Ich und seiner mathematischen Architektonik.
Zunächst wird es darum gehen, die starre Struktur des Euklidischen Raumes, der für 2000 Jahre als die einzig möglich geometrische Struktur galt, aufzubrechen und tiefer liegende Schichten freizulegen.
“Tieferlegung der Fundamente” (David Hilbert)
1. Schritt: Aus einem Euklidischen Raum wird ein Projektiver Raum
Da sich das menschliche Bewusstsein nicht mehr als 3 Dimensionen anschaulich vorstellen kann, soll zunächst der 3-dimensionale Euklidische Raum auf eine 2-dimensionale Euklidische Ebene reduziert werden. Dann wird ein fester Punkt Z außerhalb der Ebene als Zentrum gewählt. Jetzt verbinden wir jeden Punkt P der Ebene mit diesem Zentrum durch eine Gerade G. Aus den Punkten sind Geraden durch ein festes Zentrum geworden und sie tragen den Namen “eigentliche Punkte”. Die Geraden G, welche auch durch das Zentrum gehen, denen aber kein Punkt der Euklidischen Ebene entspricht, da sie parallel zu dieser verlaufen, heißen “uneigentliche Punkte”, “ideale Punkte” oder auch “unendlich ferne Punkte”. Beim Euklidischen Raum verwandeln sich ganz analog die Punkte des jetzt 3-dimensionalen Raumes in die Geraden eines 4-dimensionalen Raumes, welche durch ein festes, außerhalb des Raumes liegendes Zentrum gehen. Die Menge aller Geraden, die durch einen festen Punkt gehen, heißt auch Geradenbündel.
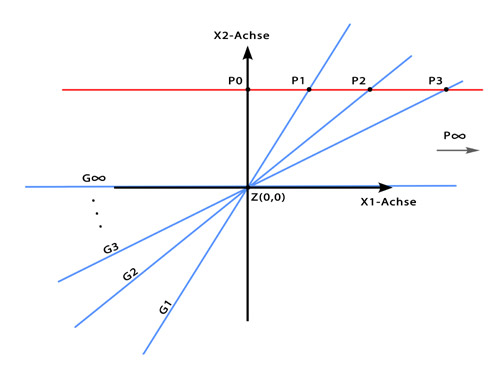
(Bild: Polaris Hörspiele)
2. Schritt: Die Geraden erhalten eine Richtung
Verläuft die Richtung der Geraden von den Punkten des Euklidischen Raumes hin zum Zentrum Z, so hat man es mit Sehstrahlen (Perzeptionen) zu tun. Das Zentrum, durch das sie gehen, ist dann ein Sehpunkt (focus imaginarius), und der Euklidische Raum selbst kann als die 3-dimensionale Bildebene einer Zentralperspektive im 4-dimensionalen Raum interpretiert werden.
Wir können die Geraden aber auch genau umgekehrt orientieren, vom Zentrum weg in Richtung 3-dimensionaler Bildebene. Dann werden aus den Geraden Lichtstrahlen, und der Euklidische Raum verwandelt sich (im übertragenen Sinne) in die Felswand (als Projektionsfläche) von Platons Höhle mit der Materie als Schatten darauf. Das Projektionszentrum befindet sich unsichtbar im Rücken der Höhlenbewohner, gleichsam in der 4. Dimension.
An dieser Stelle ist natürlich auch an Flatland – A Romance of Many Dimensions (dt. Titel „Flächenland“) von Edwin Abbott Abbott zu erinnern (siehe Hyperraum 2).
3. Schritt: Kegelschnitte als Horizonte
In der Euklidischen Geometrie wird der Abstand zwischen zwei Punkten mit Hilfe des Pythagoreischen Lehrsatzes gemessen.
Gauß, Bolyai, Lobatschewski und andere haben aber auch Nichteuklidische Geometrien (z.B. Hyperbolische und Elliptische Geometrien) entworfen, in denen der Abstand ganz anders gemessen wird. Woher also nimmt die Mathematik ihren Maßstab für Längenmessung? Es ist erstaunlicherweise ein Horizont. Er legt als ein invariantes Gebilde sowohl die Art der Geometrie fest, als auch, was innerhalb dieser überhaupt als ein geometrisches Objekt (als eine Invariante der zugehörigen Transformationsgruppe) zu gelten hat. Das ist im Wesentlichen (sehr verkürzt) das Erlanger Programm von Felix Klein.
Betrachtet man die Projektive Geometrie als eine Gattung, dann sind die Euklidische Geometrie und die Nichteuklidischen Geometrien Arten, die durch Spezifizierung bestimmter Horizonte (Kegelschnitte) aus der Projektiven Geometrie hervorgehen.
Es ist kein Zufall, dass solche Horizonte an Kants “transzendentale Bedingungen der Möglichkeit der Erfahrung” erinnern, die als Anschauungs- und Denkformen die (Erfahrungs-) Materie bestimmen. Diese Parallele wird uns als roter Faden dienen und noch intensiv beschäftigen.
Wie sieht ein solcher Horizont im Projektiven Raum nun konkret aus? Im Falle der ebenen Hyperbolischen Geometrie ist es zunächst ein Kegel, der mit seiner Spitze im Zentrum des Geradenbündels liegt. Da, wo dieser Kegel eine Ebene in Form eines Kreises (oder auch Ellipse, Hyperbel oder Parabel) schneidet (reelle Schnittfigur), ist der Horizont der Hyperbolischen Geometrie. Die Punkte der Ebene innerhalb solch einer reellen Schnittfigur bilden dann die “Materie der Geometrie”. Wird durch zwei solche Punkte im Innern eine Gerade gelegt, dann schneidet diese den Kreis (bzw. Horizont) in zwei weiteren Punkten. Aus diesen vier Punkten kann mit Hilfe des sogenannten Doppelverhältnisses der Abstand zwischen den zwei Punkten im Inneren berechnet werden.
Hält man den einen inneren Punkt fest und lässt den Zweiten Richtung Horizont wandern, wird der über das Doppelverhältnis definierte Abstand immer größer, bis er schließlich am Horizont unendlich ist.
In der Elliptischen Geometrie sind die Verhältnisse ganz analog, nur, dass dort ein imaginärer (nullteiliger) Kegelschnitt zur Anwendung kommt.
Entartet der Kegelschnitt zu einem singulären Kegelschnitt, so findet man die Euklidische Geometrie wieder.
(mehr dazu im mathematischen Anhang, am Ende der Seite, unter Punkt 1 und 2)
Diese Horizonte generierenden Kegel (projektive Quadriken) werden in Zukunft auch “projektive Lichtkegel” genannt. Sie teilen das Geradenbündel in drei Bereiche: in raum-, zeit- und lichtartige Geraden. Projektive Lichtkegel sind für das Verständnis des Zusammenhangs zwischen Kants Transzendental-Philosophie und der Theoretischen Physik von zentraler Bedeutung und werden in Zukunft noch eine wichtige Rolle spielen.

(Bild: Wikipedia)
4. Schritt: Eine kurze Zwischenbilanz
Der starre Euklidische Raum, der Raum der Newtonschen Physik, ist nur die “Projektionsleinwand” eines wesentlich umfassenderen und allgemeineren Raumes: des Projektiven Raums. Das Zentrum dieses höheren Raumes, der Sehpunkt, ist der Archimedische Punkt, nach dem schon Descartes (siehe Horizonte 3) gesucht hat, das anschauende Ich. Bezeichnen wir die im Sehpunkt sich schneidenden (fokussierenden) Sehstrahlen als Perzeptionen (Wahrnehmungen), dann wird schnell die Nähe zu Leibniz und Kant erkennbar.
Um aber wirklich bis zu Kants transzendentaler Apperzeption (siehe Horizonte 7A und Horizonte 7B) hinaufsteigen zu können, muss auch das Fundament des Projektiven Raumes noch tiefer gelegt werden (Grassmann- bzw. Clifford-Algebra, konforme Kompaktifizierung usw.).
Zwischen Mathematik, Physik und Philosophie bestehen keine unüberwindlichen Gräben. Das gegenseitige Nichtverstehen ist eher ein Übersetzungsproblem.
“Auf der Suche nach der verlorenen Zeit” (Marcel Proust)
5. Schritt: absolute Zeit, relative Zeit, Gedächtniszeit
Newtons Raum ist der Raum der Euklidischen Geometrie und er ist ein absoluter Raum. Ebenso ist die Zeit für Newton eine absolute Zeit. Das will besagen, dass der räumliche Abstand und die zeitliche Dauer, die für die Newtonsche Physik essentiell sind, vom Beobachterzustand (Geschwindigkeit, Ort, Richtung … ) als unabhängig (d.h. invariant) angenommen werden. Experimente haben aber gezeigt, dass bei Geschwindigkeiten nahe der Lichtgeschwindigkeit sich Raum- und Zeitabstände ändern und somit keine absoluten, sondern nur noch relative Größen sind. Das hat Einstein dazu veranlasst, die Galilei-Transformationen, die bisher die “Übersetzungsarbeit” zwischen bewegten Beobachtern leisteten, durch die Lorenz-Transformationen zu ersetzen. Eine wesentliche Konsequenz daraus war, dass Newtons Raum und Zeit durch eine Union beider, die Raumzeit (4-dimensionaler Minkowski Raum) ersetzt werden mussten. Aufgespannt wird dieser Raum von 3 räumlichen und einer zeitlichen Achse. Im Nullpunkt dieses Koordinatensystems befindet sich der Beobachter des physikalischen Geschehens. In dieser Raumzeit gibt es einen zweifachen Lichtkegel, bestehend aus Vergangenheits- und Zukunftslichtkegel, deren beide Spitzen sich im Koordinatenursprung und damit am Ort des Beobachters berühren. Dieser Doppel-Kegel ist Ausdruck der Kausalstruktur (Ursache und Wirkung) des Minkowski Raumes.
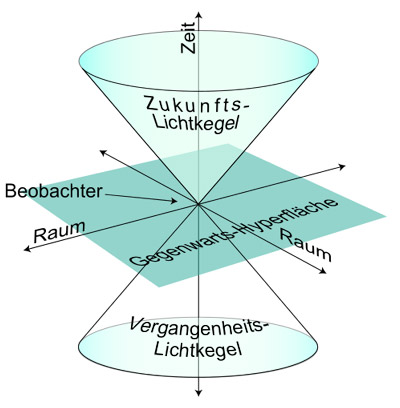
Der Lichtkegel des Minkowski Raumes darf nun nicht mit dem Lichtkegel des Projektiven Raumes verwechselt werden. Der Minkowski Raum ist, wie der Euklidische Raum, ein durch einen Horizont definierter metrischer Raum. Anstelle der euklidischen Metrik (Abstandsfunktion) herrscht in ihm aber eine sogenannte pseudoeuklidische Metrik. Ansonsten ist wieder alles wie oben:
Der Minkowski Raum ist die 4-dimensionale “Projektionsleinwand” in einem 5-dimensionalen Raum. Der 4-dimensionale projektive Lichtkegel schneidet die 4-dimensionale Projektionsleinwand in einem 3-dimensionalen Horizont. Dieser umschließt den 4-dimensionalen Minkowski Raum im Unendlichen und gibt ihm seine metrische Struktur, d.h. ein quantitatives Maß zur Bestimmung von räumlichen Abständen und zeitlicher Dauer.
(mehr dazu im mathematischer Anhang, am Ende der Seite, unter Punkt 3)
Wir haben also einerseits den empirisch-realen Beobachter im (durch ein Koordinatensystem festgelegten) Mittelpunkt des Minkowski Raumes und andererseits das transzendental-ideal anschauende Ich im Zentrum des größeren Projektiven Raumes.
Um diese formale Übereinstimmung zwischen Mathematik, Physik, Kants Transzendental-Philosophie und Leibniz’ Monadologie (siehe Horizonte 6B) weiter zu vertiefen, wird es im Fortgang notwendig sein, die Struktur des Projektiven Raumes weiter auszubauen. Die Clifford-Algebra wird sich dabei als ideales Werkzeug und natürliche Sprache erweisen. Materie und Form der Philosophie Kants werden wir in einem ersten Ansatz in Gerade und Hyperebene (beide durch das Zentrum des Projektiven Raumes gehend) übersetzen. Der projektive Lichtkegel wird dabei als eine sowohl Materie und Form, Innen und Außen, als auch Raum und Zeit in Beziehung setzende Polarität erkannt werden. Das ist in Kants Sprache die Apprehension, die synthetische Kraft der transzendentalen Apperzeption auf der Ebene der sinnlichen Anschauung.
Damit es aber wirklich gelingt, alle Stufen der Bewusstseins-Pyramide bis hinauf zu ihrer Spitze, der transzendentalen Apperzeption, zu erklimmen, muss der Projektive Raum auch noch um eine zusätzliche Dimension (eine Art Gedächtniszeit) erweitert werden. Aber wie bei jeder – nicht immer einfachen – Bergbesteigung, belohnt dann schließlich der weite Ausblick.
Mathematischer Anhang
Punkt 1
Metrische Geometrien der Ebene und ihre projektiven Lichtkegel (Horizonte) in homogenen Punktkoordinaten:
Hyperbolische Geometrie (reeller Kegelschnitt):
Elliptische Geometrie (imaginärer Kegelschnitt):
Euklidische Geometrie (entarteter Kegelschnitt):
Minkowski Geometrie:
De-Sitter Geometrie:
Anti-de-Sitter Geometrie:
Die Euklidische-Ebene ist ein 2-dimensionaler Vektorraum und Punkte werden durch die Vektoren dargestellt. Der euklidische Abstand berechnet sich mit Hilfe des pythagoreischen Lehrsatzes zu
Es gilt
Punkt 2
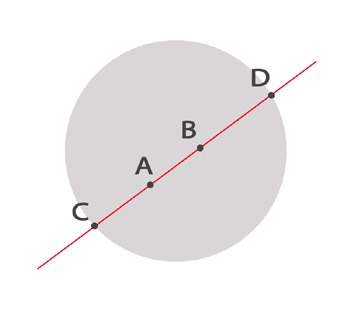
Sind zwei Punkte der Kreisscheibe, so trifft die durch
verlaufende Sehne den Kreis (Horizont) in zwei Punkten
. Der hyperbolische Abstand von
wird nun mit Hilfe des Doppelverhältnisses
berechnet:
Punkt 3
Die Pseudoeuklidische Geometrie des 4-dimensionalen Minkowski Raumes wird durch folgenden projektiven Lichtkegel definiert:
bis
sind die homogenen Punktkoordinaten des Projektiven Raumes (ein 5-dimensionaler Vektorraum), durch dessen Zentrum
die Geraden verlaufen.
Der Minkowski Raum ist ein 4-dimensionaler Vektorraum. Er liegt auf der durch die Bedingung festgelegten Projektionsebene (eine Hyperebene im Projektiven Raum) und seine Punkte werden durch die Vektoren
dargestellt.
und
sind die durch den projektiven Lichtkegel definierten metrischen Raum-Zeit-Koordinaten.
steht für die Lichtgeschwindigkeit.
Das Quadrat des pseudoeuklidischen Abstandes im Minkowski Raum (der 4-dimensionale Abstand zweier Ereignisse) ist gegeben durch:
Der metrische Lichtkegel im Minkowski Raum hat die Gestalt:
Der Zusammenhang zwischen den metrischen und homogenen Punktkoordinaten ist:
Die homogenen Punktkoordinaten des empirisch-realen Beobachters sind und die des transzendental-ideal anschauenden Ichs
Zur Fortsetzung: Horizonte 9 – Teil A 〉〉〉